ABSTRACT
Finding Contiguous Sequential Patterns (CSP) is an important problem in Web usage mining. In this paper we propose a new data structure, UpDown Tree, for CSP mining. An UpDown Tree combines suffix tree and prefix tree for efficient storage of all the sequences that contain a given item. The special structure of UpDown Tree ensures efficient detection of CSPs. Experiments show that UpDown Tree improves CSP mining in terms of both time and memory usage comparing to previous approaches.
Categories and Subject Descriptors
E.1 [Data]: Data Structures - Trees; H.2.8 [Database Management]: Data Mining
General Terms: Algorithms, Performance, Experimentation, Theory.
Keywords: Web usage mining, sequential pattern, contiguous sequential pattern
1. INTRODUCTION
Web usage mining provides useful information for many applications. One major technique for Web usage mining is sequential pattern (SP) mining which discovers user navigational patterns. In practice, contiguous sequential pattern (CSP, a variation of SP in which the items appearing in a sequence that contains the pattern must be adjacent with respect to the underlying ordering.) is more effective comparing to SP for applications such as Web recommendation/personalization [4]. Mining CSPs from Web logs can be taken as SP mining under two constraints. First, each element in a sequence consists of only one item. Second, items appearing in a sequence that contains a pattern must be adjacent with respect to the underlying order as defined in the pattern. Most previous approaches do not address the problem specifically, but instead they apply a general constraint description framework to solve the problem, which is inefficient due to the large searching space and inefficient data structures. In this paper a new data structure, UpDown Tree, is invented for CSP mining. An UpDown Tree combines suffix tree and prefix tree for efficient storage of all the sequences that contain a given item. The special structure of UpDown Tree ensures efficient detection of CSPs. Experiments show the effectiveness of UpDown Tree based CSP mining.
2. MINGING CSP USING UPDOWN TREE
Let P = {p1, ¡ pn} be a set of items (Web page Ids), an access sequence AS = (as1, ¡, asm) is an ordered list of page Ids, where asi Î P, i Î {1, ¡, m}. An AS a = (a1, a2, ¡ , aj) is a contiguous sub-AS of another AS b = (b1, b2, ¡ , bk), k ¡Ý j, if there exists an integer i, 1 ¡Ü i ¡Ü k-j+1, such that a1 = bi, a2 = bi+1, . . . , aj = bi+j-1. In this case a is called contained in b, denoted as a Í b. A Web access sequence database (WASD) is a set of ASs {S1, S2, ¡, Su}, where Si is an AS. The support of an AS S in WASD is defined as SupWASD(S)= |{ Si |SÍ Si }| / u. Given a positive value minSup as the support threshold, S is called a contiguous sequential pattern (CSP) in WASD if SupWASD(S) ¡Ý minSup. A CSP with length l is called an l-CSP.
Problem Statement. Given a WASD and the minSup threshold, CSP mining is to find the complete set of CSPs in the database.
2.1 Concept of UpDown Tree
Our goal is to find a data structure that supports efficient CSP mining in terms of both memory and time. Below we propose a special data structure, UpDown Tree, for this purpose.
Table 1 shows some example ASs. To detect CSPs containing an item, say 3, we need identify all the sequences that contain 3. Observing a sequence that contains 3, we know that it can be divided into two subsequences before/after 3 (the full prefix/suffix of 3). The full suffixes of 3 can be efficiently stored using a suffix trie. We call this trie a Down Trie because its root node is at the first level. For each full suffix of 3 we add its sequence Id to the Id set of the node in the Down Trie corresponding to the last item of the full suffix. The Down Trie can be further compressed into a Down Tree based on the concept of Patricia Tree [3] by merging a node with its parent if the node is the only child of its parent and the node has an empty Id set. Similarly, we can represent all the full prefixes of 3 with an Up Trie and compress the Up Trie into an Up Tree. The root node of the Up Tree is at the lowest level.
Table 1. Some example access sequences
|
Seq. Id |
AS |
Full prefix of 3 |
Full suffix of 3 |
|
1 |
3 |
3 |
3 |
|
2 |
5 8 3 4 2 |
5 8 3 |
3 4 2 |
|
3 |
2 5 8 3 4 2 |
2 5 8 3 |
3 4 2 |
|
4 |
2 5 3 4 7 |
2 5 3 |
3 4 7 |
|
5 |
7 5 3 5 4 |
7 5 3 |
3 5 4 |
Since Up and Down Tree share the same root, they are integrated into an UpDown Tree as shown in Fig. 1. To detect all the CSPs that include 3, intuitively, any such CSP corresponds to a path in the UpDown Tree that starts at a node in the Up Tree. Thus we can decompose the problem into finding all the CSPs starting at any node in the Up Tree, which can be efficiently solved as described in Algorithm 1 below. Taking a depth first order to detect CSPs starting from every node in the Up Tree, we can implement a top down approach for CSP mining which is more efficient than traditional bottom up approach because it eliminates unnecessary candidate checking based on Apriori rule [1].
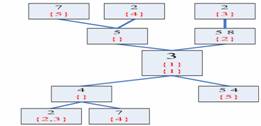
Figure 1. An example UpDown Tree.
2.2 UpDown Tree based CSP Mining
Problem partitioning. Let {<x1>, < x2>, ¡, <xt>} be the complete set of 1-CSPs in a WASD, x1 < x2 < ¡ < xt., based on apriori rule [1], any CSP only contains items in the set of {x1, x2, ¡, xt}. Given the set of all the CSPs, first we create t empty sets. We then remove all the CSPs that contain xt from the CSP set to set t, and in the resulted CSP set we remove all the CSPs that contain xt-1 to set t-1, ¡. We continue this process until removing all the CSPs that contain x1 from the CSP set to set 1. Now the original CSP set is empty. In this way we partition the CSP set into t disjoint set, and set i (1 ¡Ü i ¡Ü t) is the set of CSPs that contains xi and items smaller than xi.
Algorithm 1 Detecting all the CSPs that contain an item xi.
Input/output: UpDown Tree of xi/All the CSPs that contain xi
Method: 1) Create an empty CSP set for xi. For each node k in the Up Tree in depth first order,
1.1) Create an empty CSP leaf set and get the ending nodes of all sequences in the Id set of k in the Down Tree. For each ending node, put the Ids of all the sequences that end at it in its endIdSet;
1.2) Enqueue each ending node into a priority queue based on the descending order of its height in the Down Tree;
1.3) Dequeue nodes in the priority queue until the queue is empty. For each dequeued node m, if the size of its endIdSet is no less than minSup, add m to CSP leaf set, otherwise join its endIdSet to its parent¡¯s endIdSet and enqueue the parent if m is not the root.
1.4) For each node j in the CSP leaf set, create a CSP by concatenating the key d-gaps of the nodes in the path from k to j, and add the CSP to CSP set;
1.5) For the sequences that are not counted towards the support of any CSP, add their Ids to the Id set of k¡¯s parent node. ÿ
Detecting all the CSPs of a WASD Following the problem partitioning strategy discussed above, first we create an occurrence set for each frequent item. Then for each frequent item xi in descending order, we first find all the CSPs containing xi (set i) using Algorithm 1. Then for each smaller item j in the CSPs detected, we remove its corresponding occurrences from its occurrence set to simplify CSP detection for set j.
3. EXPERIMENT RESULTS
Experiments were performed on a 1.8G Hz Pentium-M Laptop with 1 GB memory. We compare our approach with GenPrefixScan which is among the best ones for SP mining with gap constraints [2]. The testing datasets are generated by AssocGen [1], a standard data set generator for SP mining. The datasets contain 50-500K sequences (D) and 10,000 different items. The average length of sequences is 50. The average length of patterns is set to 8, and the number of patterns is set to 5000.
Fig. 2 (a) shows experiment results on time usage. Both approaches scale up linearly as D increases. UpDown Tree outperforms GenPrefixScan by a factor of more than 5. Fig. 2(b) shows experiment results on memory usage. UpDown Tree approach scales up sub-linearly as D increases. GenPrefixScan approach scales up more than linearly. Both have similar memory usage when D is small. As D is increased to 500K, UpDown Tree outperforms GenPrefixScan by a factor of more than 5.
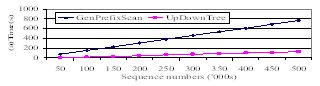
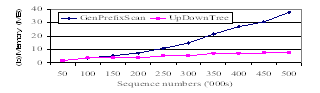
Figure 2. Time/memory usage on different sequence numbers.
The reasons that our approach performs better is as follows, (1) The top down approach of our method eliminates unnecessary candidate checking by detecting the longest CSP first; (2) Instead of storing each sequence separately, UpDown Tree compresses the full prefixes/suffixes of each item and merges some certain nodes with their children, both can effectively reduce memory consumption.
4. CONCLUSIONS
In this paper a new data structure, UpDown Tree, is invented to solve the problem of Web log CSP mining. Experiment results show that UpDown Tree based approach performs much better in terms of both time and memory comparing to GenPrefixSpan, one of the best existing approaches for CSP mining.
5. REFERENCES
[1] Agrawal R. and Srikant R. Mining sequential patterns. In Proceedings ICDE'95 (1995). 3-14.
[2] Antunes C. and Oliveira A. L. Sequential pattern mining algorithms: Trade-offs between speed and memory. In 2nd Workshop on Mining Graphs, Trees and Seq. (2004).
[3] Morrison D.R. Practical Algorithm to Retrieve Information Coded in Alphanumeric. J. ACM, 15 (1968), 514-534.
[4] Nakagawa M. and Mobasher B. A Hybrid Web Personalization Model Based on Site Connectivity. In WEBKDD 2003 (2003). 59-70.
|
Copyright is held by the author/owner(s). WWW 2007, May 8¨C12, 2007, Banff, Alberta, Canada. ACM 978-1-59593-654-7/07/0005. |