WWW 2007, May 8-12, 2007,
A Kernel based Structure Matching for Web Services Search
Jianjun Yu Shengmin Guo Hao Su Hui Zhang Ke Xu
State Key Lab. of Software Development Environment
Abstract:
This paper describes a kernel based Web Services (abbreviated as service) matching mechanism for service discovery and integration. The matching mechanism tries to exploit the latent semantics by the structure of services. Using textual similarity and n-spectrum kernel values as features of low-level and mid-level, we build up a model to estimate the functional similarity between services, whose parameters are learned by a Ranking-SVM. The experiment results showed that several metrics for the retrieval of services have been improved by our approach.
Categories and Subject Descriptors
H.3.3 [Information Storage and Retrieval Information]: Search and Retrieval - retrieval models, search process, selection process
H.3.5 [Information Storage and Retrieval]: Online Information Services - Web-based Services
General Terms
Algorithms, Languages, Design, Experimentation
Keywords
Web Services, Web Services Matching, WSDL, n-Spectrum Kernel, Ranking SVM
1. Introduction
A hotspot in the research of service is to realize large-scale service discovery and integration in Internet. Conventional matching mechanisms, like in UDDI, are mainly based on keyword search, however, the precision of those approaches are relatively low. To address this problem, several approaches considering structural information have sprung up [1,3,6]. They significantly improve the precision with the requirement that matched services should be similar in structure. But in practical, those approaches are too strict to recognize similar services with different data structure encapsulation. Consequently, they have low recalls.
Therefore, we put forward a novel loose tree matching algorithm which extracts the structural features from another perspective to help improve the recognition of functionally similar services.
2. Web Services Similarity
In our algorithm, services are schemed by WSDL (Web Services Description Language) as tree-structured documents, and two kinds of features are extracted.
One kind is to calculate two WSDL documents' text
similarity with a classical VSM (Vector Space Model) [2], regarding the documents as
unstructured text. In the classical VSM, a document is formalized as a vector,
and each dimension of the vector represents a word in the document. The value
of the dimension is calculated by the ![]() formula [2] as an estimation of the importance
of the word in the document.
formula [2] as an estimation of the importance
of the word in the document.
The other kind of features describes the structural
similarity. It takes two steps to get such features. First, we have to do some
preprocess to extract document trees from the two WSDL documents and align
their nodes according to the label's textual similarity. Aligned nodes are
considered identical. After the preprocess, we model the documents trees as a
vector in a n-spectrum vector space ![]() , and use the
newly brought forward n-spectrum kernel function [4] to compare how much hierarchical
relationships the two trees share in common. With a set of different
, and use the
newly brought forward n-spectrum kernel function [4] to compare how much hierarchical
relationships the two trees share in common. With a set of different
![]() , we have a set of different function values as features.
, we have a set of different function values as features.
Modeling a document tree as a vector in the n-spectrum vector space is similar to modeling a text document stated above, except that each dimension in the n-spectrum vector space represents an n-path subsequence defined as below:
A path subsequence (abbreviated as
![]() ) is an ordered set of nodes extracted from a path of
the document tree (abbreviated as
) is an ordered set of nodes extracted from a path of
the document tree (abbreviated as ![]() ). The set containing
all
). The set containing
all ![]() (
(![]() is the number of nodes in a
is the number of nodes in a ![]() ) of the
) of the ![]() is called the n-spectrum of
is called the n-spectrum of ![]() , denoted by
, denoted by ![]() . Intuitively, two document trees are more similar if they share
more common
. Intuitively, two document trees are more similar if they share
more common ![]() .
.
Then, we consider the problem of a ![]() weight in
the vector. A
weight in
the vector. A ![]() may not be picked contiguously from a path, however, we assume that contiguous picked ps should weigh more. So, we define a decay factor
may not be picked contiguously from a path, however, we assume that contiguous picked ps should weigh more. So, we define a decay factor ![]() to weight the presence of gap in a
to weight the presence of gap in a ![]() . For the indices
. For the indices ![]() identifying
the occurrence of a
identifying
the occurrence of a ![]() in a document tree
in a document tree ![]() , we use
, we use ![]() to denote the distance between the first node and the last node in
the corresponding path, namely, the difference of their depth in the tree. In
the gap-weighted kernel, we weight the occurrence of the
to denote the distance between the first node and the last node in
the corresponding path, namely, the difference of their depth in the tree. In
the gap-weighted kernel, we weight the occurrence of the ![]() with
the exponentially decaying weight
with
the exponentially decaying weight ![]() .
.
With the set of ![]() and their weights in
the vector, we can give the formula of n-spectrum kernel value:
and their weights in
the vector, we can give the formula of n-spectrum kernel value:
DEFINITION 1 (GAP-WEIGHTED N-SPECTRUM). The feature space F associated with the gap-weighted spectrum
kernel of n-ps is indexed by ![]() (the
set of all n-
(the
set of all n-![]() ), with the embedding
), with the embedding ![]() given
by
given
by
![]()
Where p is the indices identifying the occurrence of ![]() . The associated kernel is defined as:
. The associated kernel is defined as:
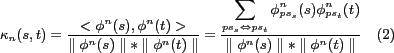
where ![]() and
and ![]() .
.
With the textual and structural similarities, we can
estimate the functional similarity as follows:
![]()
where ![]() ,
, ![]() and
and ![]() are
two services,
are
two services, ![]() and
and ![]() are their
corresponding document trees,
are their
corresponding document trees, ![]() is their textual similarity, and
is their textual similarity, and ![]() is the gapped i-spectrum kernel
describing their structural similarity.
is the gapped i-spectrum kernel
describing their structural similarity.
The parameters ![]() are estimated by
the Ranking SVM [7]. Ranking
SVM is brought forward by machine learning researchers in recent years to solve
ordinal regression problem, and it has been proved to be effective [7]. In this paper, the retrieval of
matched services is formalized as a ''learning to rank'' problem, where the
matching degree between query and returned services are mapped into three
ordered categories (ranks). We have three features in the ranking problem: text
similarity, 2-spectrum and 3-spectrum kernel values, and their weights are in
Equation (3). Our experiment result shows that the best values of
are estimated by
the Ranking SVM [7]. Ranking
SVM is brought forward by machine learning researchers in recent years to solve
ordinal regression problem, and it has been proved to be effective [7]. In this paper, the retrieval of
matched services is formalized as a ''learning to rank'' problem, where the
matching degree between query and returned services are mapped into three
ordered categories (ranks). We have three features in the ranking problem: text
similarity, 2-spectrum and 3-spectrum kernel values, and their weights are in
Equation (3). Our experiment result shows that the best values of ![]() are
are ![]() and the best values of
and the best values of ![]() are
are ![]() in our
data sets.
in our
data sets.
3. Experiments and Evaluation
The experiment data set of services is collected from WWW, containing 2,140 valid services in total.
In this paper, we define three categories for the judgment of the matching degree between the query and the WSDL documents: 'good, 'insignificant' and 'bad'.
Generally, we hope that a good return can be modified with little effort to replace the query in Web environment. Therefore, it should provide almost the same function to the query. A bad return may only be textually similar to the query document with no obvious structural similarity. An insignificant return is the one with a similarity degree between good and bad.
As a baseline method, we simply use the text similarity to rank and categorize the candidates into three categories. This method does not take structural information into consideration at all. As another baseline method, we use the Edit Distance from Gabriel Valientes book [5] to get the similarity between WSDL documents.
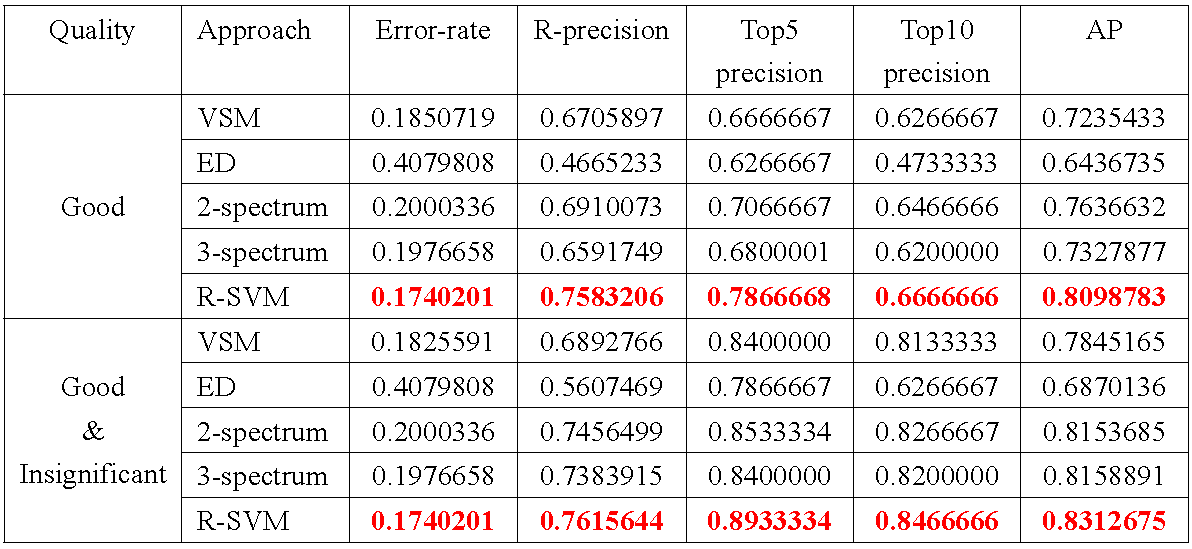
We made use of four evaluation metrics, which are ''error rate'', ''R-precision'', ''Top-N precision'', and ''Average precision''. The evaluation result on the test set is listed in Figure 1.
We have our evaluation on two levels. The first group is evaluated using 'good', while the second group is evaluated by replacing 'good' with 'good' and 'insignificant'. Taking a closer look at Figure 1, we notice that Ranking-SVM outperforms other approaches in every metric. As an interpretation of the result, we may regard VSM as low-level feature and 2-spectrum and 3-spectrum as mid-level features with structural information. The low-level feature is directly extracted from WSDL with less deeper semantic and less noise, while mid-level features reflect deeper semantic with more noises. Ranking-SVM combines VSM, 2-spectrum kernel and 3-spectrum features together, so that low-level feature and high-level features complement each other; as a result, it outperforms all other methods. We may also notice that the R-precision and Top-5 precision for 'good' are relatively equal. In fact, the average number of relevant documents to the queries is approximately 5.
4. Conclusion
In this paper, we present a novel approach for services matching problem. In order to achieve the task, we model WSDL documents in the vector space and then defined the gapped n-spectrum kernel function in the space. Using textual similarity and n-spectrum kernel values as features of low-level and mid-level, we build up a model to estimate the functional similarity between services, whose parameters are learned by a Ranking-SVM. Experimental results indicate that our model significantly outperforms other methods. Since the n-spectrum kernel function is defined in vector space, the framework of our approach can be easily adapted to matching problems of other domains.
5. REFERENCES
D.
Searching XML Documents via XML Fragments.
In the Proceedings SIGIR'03, 2003.
B. Everitt.
Cluster Analysis. 2nd edition.
N. Kokash.
A Comparison of Web Service Interface Similarity Measures.
J. Shawe-Taylor and N. Cristianini.
Kernel Methods for Pattern Analysis.
G. Valiente.
Algorithms on Trees and Graphs.
Y. Wang,
S. Eleni, O. M. E., W. Sanjiva, P. M. P., and J. Yang.
Semantic Structure Matching for Assessing Web Service
Similarity.
In the Proceeding of ICSOC'03, 2003.
J. Xu, Y. Cao, H. Li, and M. Zhao.
Ranking Definitions with Supervised Learning Methods.
In the Proceedings of WWW, 2005.